Edits / Updates:
  • current_height is to the harness not to the feet
  • The halving stops when dist <=1, not <1.
Due two hours prior to your scheduled lab section next week.

Goals for this homework

  • Practice the C development cycle
  • Write a small C program to get used to the syntax.
  • Write programs that exercise functions and control.

You are expected to complete this assignment individually. If you need help, you are invited to come to office hours and/or ask questions on piazza. Clarification questions about the assignments may be asked publicly. Once you have specific bugs related to your code, make the posts private.

Another note about Piazza. Piazza is your community resource - please use those as discussions amongst yourselves. We are not monitoring it all day, rather we each have check-in times once a day. Therefore, you need to start early enough to wait for feedback and/or build a vibrant, supportive community that helps each other while we are completing other necessary tasks (research, developing assignments, preparing for lecture, performing advising tasks, etc.).

Make sure you filled out the Student Information Form

This homework has several exercises. We are also providing you with some resources on printf and error handling for this assignment.

Homework 1, which includes warmup 1, will be collected from your subversion repository two hours before your scheduled lab section.

You should submit five files for this assignment (hw1.h, hw1.c, hw1_main.c, errors.txt, and Makefile) in your subversion repository as directed below. Your subversion repository is named CNET-cs152-win-16 and you can check it out with the following command: 

  $ svn checkout https://phoenixforge.cs.uchicago.edu/svn/CNET-cs152-win-16
(where CNET is your cnet). Do not commit any executable, a.out or any other, to your repository; we will (in fact, must) recompile your code on our own machines on our end.

printf

The printf() function takes a string as its first argument. The contents of this string are printed to the screen as-is, but with the same kinds of escape conventions as we saw in Racket (e.g., \n is the newline character). The function can be used with a string and no other parameters: 

  printf("Hello, world!\n");

If you want to include a representation of the value of one or more expression in the string printed by printf, you need to include one or more format codes in printf's string argument, and you need to pass correspondingly many expressions as additional arguments to printf, separated by commas. Some examples follow.

Format codes begin with the character % and the next character(s) specify the type of the value to be printed. For now, it suffices to know that d specifies an int, and lf specifies a double. To be clear, put together, we write %d as a placeholder when we want to write an int, %ld for a long int, and %lf for a double.

For example, 

  printf("The number is %d.\n", 42);
prints this: 
  The number is 42.

If we want more than one expression included in the same string, we use multiple format codes and pass arguments in lockstep with those codes: 

  int ndigits = 6;
  double approx_pi = 3.14159;
  printf("Pi to %d digits is %lf, and pi squared is %lf\n",
         ndigits, approx_pi, approx_pi * approx_pi);

Error Handling

Error handling capabilities vary by language, and what you want to do in an error varies by the situation. When an error occurs in a function, the question becomes, what should you do, and how do you notify the caller that an error occurred?

In C, there is no good way to distinguish error conditions from normal execution. This is a exercise because if you write a function, and it's used in a variety of different circumstances, it is bad programming practice to determine within the function what will be done. For example, one program might want to exit, whereas another might want to notify the user that there was bad input and to try again.

In this course, we will print the error message in a special way (see below). If there is an opportunity, we will designate a specific return value for an error condition. If there is no available return value, then we will exit from within the function.

When we print error messages, it is helpful and appropriate for them to be routed through a special error mechanism. This gives them priority, increases their likelihood of being printed in the case of a program crash, and allows them to be separated from other output. To accomplish this, we use a variant of printf called fprintf. This function works the same as printf, but takes in an extra argument at the beginning: the "file" to which to write the message. Passing in stderr as that argument will send the output to the screen, but using the special error mechanism: 

  fprintf(stderr, "error: too many widgets for the number of grommets\n");
  fprintf(stderr, "error: need ten boondoggles, but only have %d\n", num_bds);

Sometimes, these lines will be followed by exit(1); This immediately exits the program and returns a code. If you were writing a large program, you might assign a different code to each type of error that would result in an exit.

Types

The homework exercises follow. We use the type int for integers (except, in certain cases made explicit below, unsigned int), double for floating-point numbers (i.e., non-integers), and int for Booleans (noting that C has no Boolean type).

Makefile

Because you are adding a second set of files to your directory, you need to add a second target to your Makefile. In your makefile, add another two lines (with a space between these and the ones already there). 
hw1: hw1.h hw1.c hw1_main.c
	clang -Wall -o hw1 hw1.c hw1_main.c
To compile, type: 
make hw1

Set Up

The first thing to do is to create a skeleton project that will minimally execute. This week, I provided it for you. In the future, you will be expected to create it for yourself. These are the steps you will take during future pre-labs to set up your project:
  • Step 1: hw1.h. Add prototypes for all functions in this assignment. For example: 
    double surface_area_cylinder(double height, double radius);
  • Step 2: Create hw1.c. For each function, print to stderr the fact that it is not yet implemented and return with the right type. For example: 
    double surface_area_cylinder(double height, double radius)
{
	fprintf(stderr,"surface_area_cylinder not yet implemented\n");
	return 0.0;
}
  • Step 3: Create hw1_main.c. For each function, put in a single function call. For example: 
    int main()
{
	double dval;

	dval = fall_ground_distance(10, 3.2, 4);
}

First get this compiling and running. It won't print out anything, but this will mean that your code will compile and execute with our infrastructure. This must work in order to get any points in this course. Do this first, not last.

Exercise 1: Mortgage Calculator

Type "mortgage calculator" into a search engine, and several links will send you to calculators that will calculate your monthly payment given the original loan total and the number of months of the loan.

Context: Mortgages have several aspects to them. You pay a down payment, and the rest is the loan amount of L dollars. You are expected to pay off that loan after n months. You pay the same amount everything month, which is weird, because you owe more at the beginning than the end. This means that at the beginning, you are paying more interest and less towards the balance of the loan. Near the end of the loan, you are paying very little interest and the rest towards the loan balance. Figuring out what payment will pay off the loan in n months is the challenge!

The following formula is used to calculate the fixed monthly payment (P) required to fully amortize a loan of L dollars over a term of n months at a monthly interest rate of c. [If the quoted rate is 6%, for example, c is .06/12 or .005]. P = L[c(1 + c)^n]/[(1 + c)^n - 1] The next formula is used to calculate the remaining loan balance (B) of a fixed payment loan after p months. B = L[(1 + c)^n - (1 + c)^p]/[(1 + c)^n - 1] Note that in this assignment, the interest is defined as a monthly interest, not quoted rate, so you need not divide by 12.

More information at: http://www.mtgprofessor.com/formulas.htm

The function header must be as follows: 

double fixed_monthly_payment(unsigned int dollars, double interest, 
			unsigned int months);
double loan_balance(unsigned int dollars, double interest, 
			unsigned int init_months, unsigned int months);

See hw1.h for more information. If someone enters 6 for interest, that is 6%. Likewise, if someone enters 0.1, that is 0.1%, not 10%.

If the user enters a negative number for the interest, print out an error "error (function_name): [description of error]". Remember, as described above, to use fprintf rather than printf and send the output to stderr. Return -1.0 to indicate that a negative input was received. Do not exit.

Don't forget to complete this portion, test it, and commit it before moving on! This means you need to write a test function and develop a suite of test cases!

Exercise 2

Context: Rock climbing is a fun but sometimes dangerous sport. You wear a harness with a rope connected to you, the climber, and another climber, the belayer. That's great if the rope is threaded through something above you (either the belayer is above you or there is a piece of hardware (an anchor) at the top of the climb). Sounds like a chicken and egg problem to me. How does the belayer or anchor get up there?!? If you're lucky, then there is a gentle walk up the back of the climb to set an anchor. If not, you need a lead climber. This person goes up the climb first, with the rope trailing beneath her. In order to protect her in the case of a fall, she puts her quickdraws into bolts along the route, threading her rope through them. This means that, most of the time, she is above the highest piece of hardware. If she falls, it will be a bit of a fall, but at least the rope will catch her when she gets far enough below the highest pieces of hardware she is connected to.

If the lead climber falls, the belayer will grab the rope to arrest the fall. The maximum distance that the lead climber can fall is equal to twice the distance between the last bolt and his/her current position, plus the length of slack left in the line by the belayer, plus the stretch of the rope. Climbing rope stretches to absorb the shock of the fall. Interestingly, the most dangerous part of such a climb is low to the ground. Why? Because you need to be below the hardware to stop your fall, and if you hit the ground before that happens, ouch!

For more information about climbing, see here. For more information just about lead climbing, see here.

We are going to simplify the scenario for the purposes of this exercise. We will not take into account rope slack or stretch. You are to calculate the distance you'll be from the ground if you fall during rock climbing at this point. You take in the following information:

  • h1: height that your harness is off the ground.
  • h2: the distance from your feet to your harness loop (which is tied in) at tension
  • h3: distance your harness loop is from the rest position of your last quickdraw

Your job is to calculate and return the height your feet will be from the ground if you fall

Here are some diagrams to illustrate this concept:

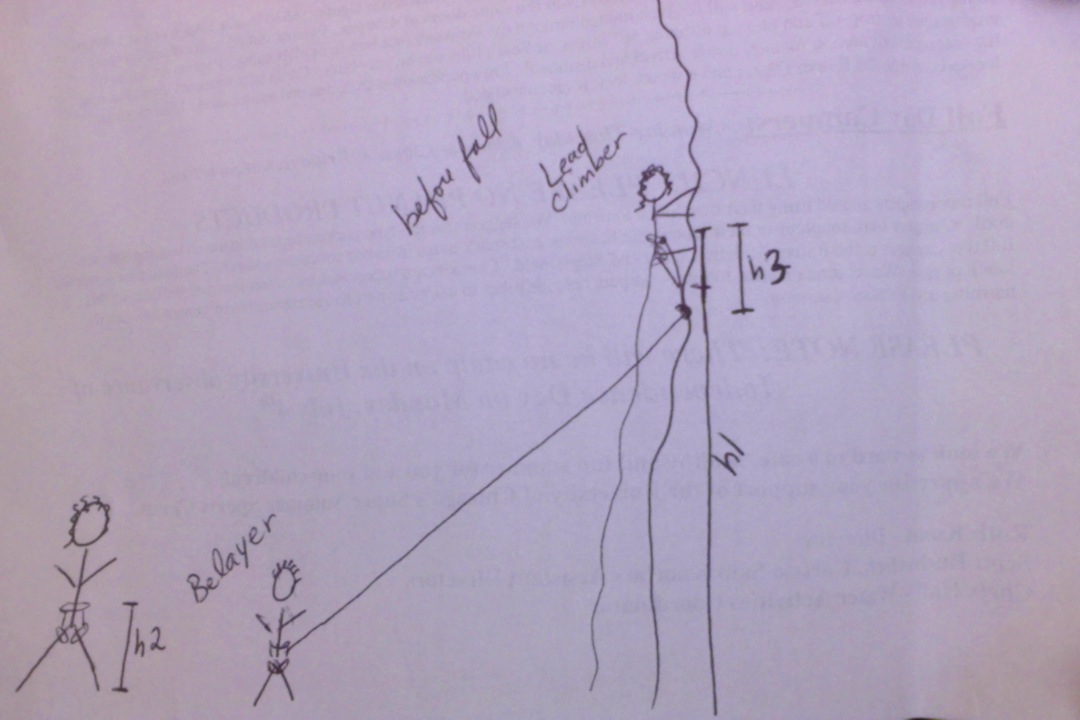
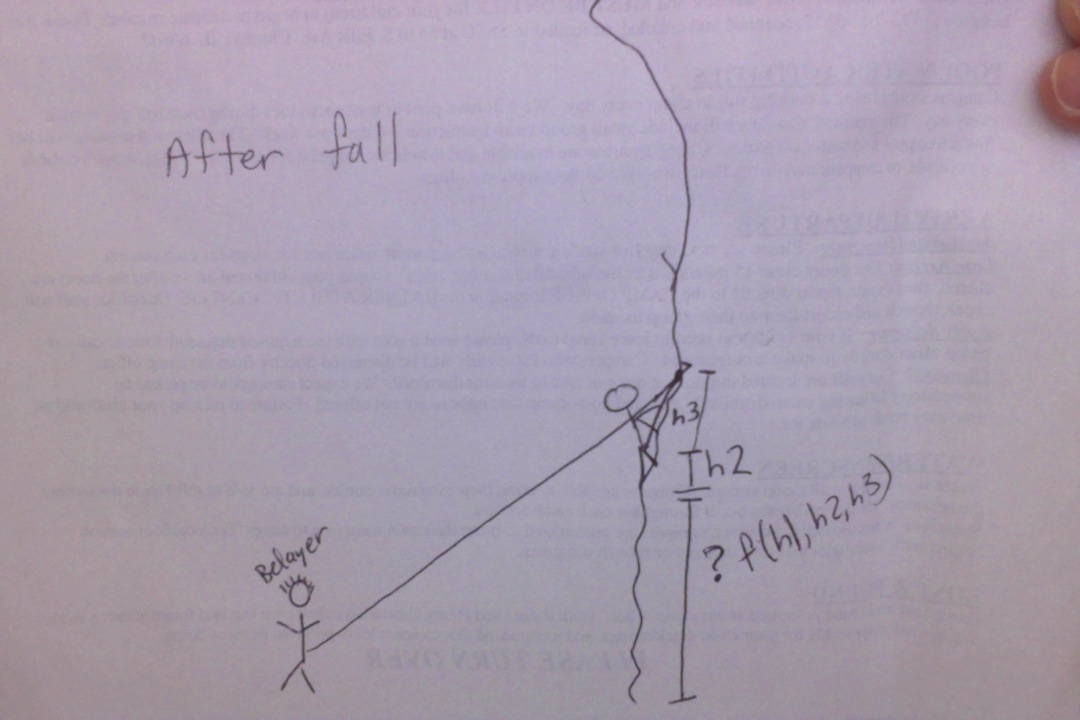
Before Fall                                 After Fall

The function header must be as follows: 

double fall_ground_distance(double current_height,
                double harness_loop_height, double clip_distance);

For this exercise, I am not going tell you the cases that result in errors. Think through all possible inputs and which inputs would be considered erroneous. As usual, if the user enters erroneous input, print out an error "error (function_name): [description of error]". Return INT_MIN. To do so, you need to #include . You can find more information about such values here: https://www.tutorialspoint.com/c_standard_library/limits_h.htm.


Don't forget to complete this portion, test it, and commit it before moving on!

Exercise 3

When exploring the idea of infinity and halving, one example used with a small child is to tell the child to stand away from you, then tell them to come halfway to you. Then do that again. Then do that again. Then you ask the child, how many times will it take for you to reach me? The answer in theory is infinity, but in reality, this is not true. There exists a distance that is too small for a child to move their foot, so they either give up and don't reach you, or close that last bit of distance.

In this problem, we are going to assume that the distance is one inch, though some children might be able to move their feet half that. Therefore, this problem asks you how many times the child will halve the distance before reaching this "end game" of being less than or equal to one inch from you.

unsigned int number_halves(float dist);
You must solve this recursively, without calling any math library functions.

Exercise 4

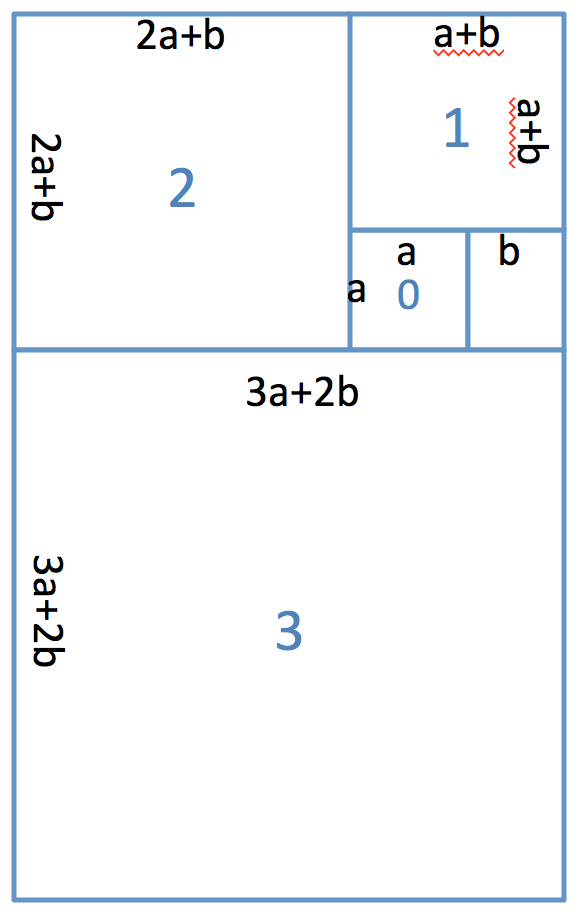
The Golden Spiral is a spiral based on the dimensions of the Golden Ratio, both which are found often in nature. For the golden ratio, we begin with a single box with length a. Then we place a rectangle next to it with the dimensions b, where (a + b) / a = a / b. If we solve this, then a/b = (1+sqrt(5))/2, or approximately 1.618.

One way to approximate the Golden Spiral is to add squares around the circle, with each square's length being the sum of the lengths of the two squares before it, as seen in the Fibonacci spiral on the above linked page. That means that, after the first rectangle of size axb is added, all subsequent additions are squares. In this case, a square of size (a+b)x(a+b) will be added, making a rectangle that is (a+b) x ((a+b)+a), and the next is (a+b+a) x ((a+b+a)+(a+b))

You are going to write a more generalized version of this process. Instead of requiring that a/b = 1.618, you are going to allow any arbitrary starting value for a and b. You will then calculate the dimensions of the subsequent squares that would be added on to create a structure like that in the pictures. Below is an image that illustrates the process for 3 squares.

Write a function that, given two starting values of a and b, calculates the length of the square that will be added after x applications of this ratio. In this case, the axa square is the 0th application, (a+b)x(a+b) is the 1st application, (a+b+a)x(a+b+a) is the 2nd application, and so on.

Hint: The pattern may not be obvious the above three examples. In order to see the pattern, you may need to draw the Golden Spiral, like I've done in the picture, for more than 3 squares. Calculate the length of the square as it keeps growing.

Here is the prototype for the function: 
float golden_spiral(float a, float b, int applications);

For this exercise, you *must* use recursion. Remember to view recursion as a problem-solving technique rather than a solution.

Submit

At this point, you should have done the following:
  • Created five files and filled in the proper information: hw1.h, hw1.c, hw1_main.c, errors.txt, Makefile inside your hw1 directory. 
  • $ svn add hw1.h hw1.c hw1_main.c errors.txt Makefile
  • Implemented all of your functions.
  • Compiled your executable manually and with the Makefile
  • Implemented your test cases
  • Executed your code
  • Debugged your code
  • Submitted your code: 
    $ svn commit -m "hw1 complete"