Homework 6 (80 points)

Download the skeleton file ArrayList.elm.

Problem 1: Random Access Lists

Chapter 9.2.1 describes how to implement purely functional arrays with fast (O(log n)) random access (to get and set).

First, we define a binary leaf tree to be a binary tree that contains data only at the leaves (nodes with zero children):

type alias Rank = Int
type LeafTree a = Leaf a | Branch Rank (LeafTree a) (LeafTree a)

A complete binary tree of rank r is a binary leaf tree with height r + 1 and 2^r leaves. Alternatively, a complete binary tree of rank 0 is a leaf, and a complete binary tree of rank r is a branch with two complete binary tree children of rank r − 1.

For example:

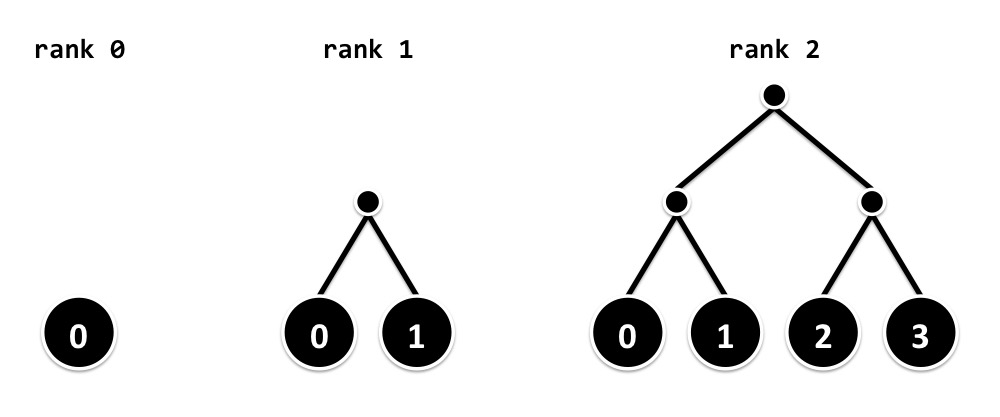
Second, we use complete binary leaf trees to represent arbitrary numbers of elements. Any number n of values can be represented with a list of at most ⌊log(n + 1)⌋ complete binary leaf trees, with at most one tree each of rank 0 to ⌊log(n)⌋.

We define the type below to capture this representation. For all operations that create and manipulate List (LeafTree a) values, we assume that the ranks are in strictly increasing order.

type ArrayList a = ArrayList (List (LeafTree a))

For example, the following three pictures show the representations of the 5 numbers 0 to 4 (left), the 6 numbers 0 to 5 (middle), and the 7 numbers 0 to 6 (right).

You may find the following helper function useful (or maybe not):

rank : LeafTree a -> Int
rank t =
  case t of
    Leaf _       -> 0
    Branch r _ _ -> r

6.1.1 --- Okasaki, Exercise 9.3 (20 points)

Implement the helper function...

consTree : LeafTree a -> List (LeafTree a) -> List (LeafTree a)

... so that it can be used to implement the cons operation.

cons : a -> ArrayList a -> ArrayList a
cons x (ArrayList trees) =
  ArrayList (consTree (Leaf x) trees)

The consTree function should run in O(log(n)) time. Your solution can assume that the only call to consTree is in cons as above.

6.1.2 --- Okasaki, Exercise 9.3 continued (20 points)

When the first element is removed from a complete binary leaf tree of rank r, the remaining elements form r complete binary leaf trees with ranks 0 to r − 1. Implement this functionality in

splitTree : LeafTree a -> (a, List (LeafTree a))

such that splitTree can be used to define head and tail as follows.

head : ArrayList a -> Maybe a
head (ArrayList trees) =
  case trees of
    [] ->
      Nothing
    t::rest ->
      let (x, ts) = splitTree t in
      Just x

tail : ArrayList a -> Maybe (ArrayList a)
tail (ArrayList trees) =
  case trees of
    [] ->
      Nothing
    t::rest ->
      let (x, ts) = splitTree t in
      Just (ArrayList (ts ++ rest))

Your splitTree function should run in O(log²(n)) time. Better yet, it should run in O(log(n)) time, but this is not required.

6.1.3 --- Okasaki, Exercise 9.3 continued (20 points)

Implement the get function

get : Int -> ArrayList a -> Maybe a

to retrieve the element at the given 0-based index, running in O(log(n)) time. If the index is out bounds, return Nothing.

Hints: Your solution needs to (i) find the appropriate LeafTree and (ii) find the appropriate Leaf within that LeafTree. The functions (^), (//), and (-) may be helpful.

6.1.4 --- Okasaki, Exercise 9.3 continued (20 points)

Implement the set function

set : Int -> a -> ArrayList a -> Maybe (ArrayList a)

to "update" the element at the given 0-based index, running in O(log(n)) time.

Grading and Submission Instructions

Submit the file ArrayList.elm updated with your changes. You are free to modify these files as you wish, as long as you do not change any type signatures that are provided.

Your solution will be graded using a combination of automated grading scripts and manual review. It is a good idea for you to design some test cases of your own to exercise more sample behaviors than just the ones provided in the writeup. We also reserve the right to take into account the organization and style of your code when assigning grades.

If you are not able to finish all parts of the assignment, make sure that all of your submitted files compile successfully. If not, you risk getting zero points for the assignment. In particular, for each file Foo.elm, make sure that it can be loaded into the Elm REPL

% elm repl
> import Foo
>

and that it can be compiled:

% elm make Foo.elm
Success! Compiled 1 module.

Submitting Your Code

Start by navigating to the folder where you checked out your repo. Next, create a subfolder for this assignment and populate it with the skeleton code:

% svn mkdir hw6
% cd hw6
% wget http://www.classes.cs.uchicago.edu/archive/2021/winter/22300-1/assignments/hw6/ArrayList.elm

If wget or a similar tool (such as curl) is not available on your machine, download and save the skeleton files provided above in some other way. Then add only these files to your repo:

% svn add ArrayList.elm

Make sure you choose the same exact names for directories and files that you create. Once you are ready to submit:

% svn commit -m "hw6 submission"

You can resubmit as many times as you wish, and we will grade the most recent versions submitted. Late days, if any, will be computed based on your submission times.

As a sanity check, you can visit the Web-based frontend for your repository to make sure that you have submitted your files as intended:

https://phoenixforge.cs.uchicago.edu/projects/USER-cs223-win-21/repository