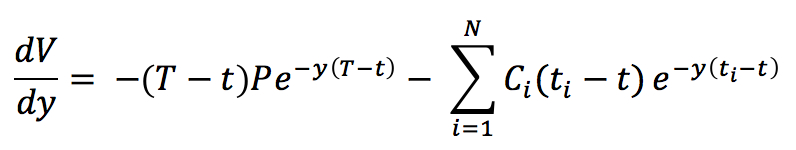
Each lab will consist of a small problem and details of  how to proceed. You need to submit labs to the TAs for grading--see submission instructions below.  Generally, unless otherwise specified, you will have one week to complete each assigned lab.

See the syllabus for information on grading.  Turning in lab assignments is required.  Submit your assignments to the subversion repository according to the directions on the syllabus page.

Lab 2   Due: 5:00 pm, Monday, April 27, 2020

Problem 1 (Composite, Strategy & Iterator Patterns): 

Consider a rudimentary fixed income pricing system.  The system is made up of Accounts.  Each account may contain both individual bonds and portfolios of bonds for clients.  The individual bonds in the account are traded as well as the bonds in the portfolios.  Your goal in this lab will be to create a simple pricing system that leverages a Composite of portfolios, bonds and multiple pricing Strategies.  Specifically, you will write your own Composite as well as an Iterator for the Composite.  You will also implement Strategies that will calculate durations for the various bonds in the Composite.  Make sure you read and thoroughly understand Gamma et. al. on the Composite, Iterator, and Strategy design patterns.  Finally, remember that the important thing is that you successfully implement the Composite, Strategy, and Iterator patterns...not that your math is flawless.  Please note that for the purposes for this lab, you may use the discrete (algebraic) versions of the formulas, as opposed to the continuous forms.

Please note that you may not use language-specific classes for your composite, strategy or iterator.  That is to say, you may not use structures such as STL lists, vectors, deques, maps, etc., nor can you use STL iterators.  You may not use Java Collections or Iterators.  You are expected to "roll your own" composite (your choice of appropriate algoritm, perhaps as a linked list), strategy and iterator.  Having said that, you certainly do not need to create expansive implementations of collections and iterators beyond what is the bare minimum to support the requirements detailed herein.

BACKGROUND:

As part of the fixed-income analytics, traders will often investigate present value, price, yield and related measures.  One of the related measures is known as the Macaulay Duration.

The derivation of the formula for calculating Macaulay Duration is given as follows: 

The slope of the price/yield curve for a coupon-bearing bond is:

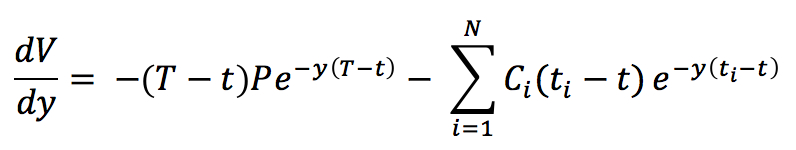
where:
            P is the principal paid at expiration T
           V is the present value of all cash payments until maturity
           N the number of coupons
            y is the constant interest rate (or yield, assuming continuous compounding)
           C_i the coupon paid on date t_i (less or equal to T)

The price/yield curve, when divided by the negative inverse of the Present Value at time t gives us:

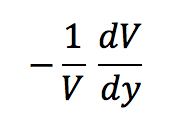
which gives us the Macaulay Duration (MD).  Traders are often interested in the sensitivity of bonds to the movement of underlying factors.  When we are dealing with smaller modulations in yield, duration gives a good first-order approximation of the change in value relative to a change in yield.  Duration is expressed in years and takes into consideration the timing of the cash flows and the size of all the cash flows.  Duration doesn't measure return, but rather, the sensitivity of a bond to a change in underlying interest rates.  We use duration to gauge how much specific bonds will increase or decrease in price if interest rates change...that is to say, it allows us to evaluate how much interest rate risk you are taking on when a new bond is bought and added to a portfolio. 

For our purposes for this lab, we can use the discrete version of the formula, yielding a slightly simplified computation:

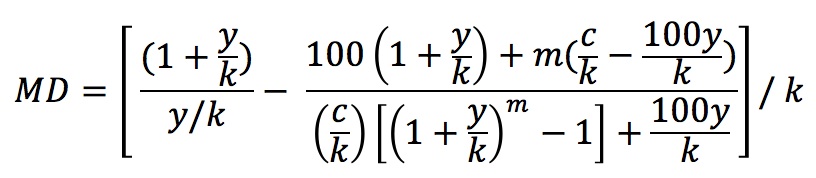
where:
            m is the number of coupons
            k the coupon frequency (no fractional payment periods)
            y is the yield per year, in decimal form, compounded at every coupon period
            c the coupon paid per year as a percentage of the principal

For example, let us assume bond μ to be a $100 2-year bond compounded semi-annually with a 5% yield with a coupon frequency of 2 (payments/year), and a coupon of 18% per year.  In this scenario, y = .05, k = 2, c = 18, and m would equal 4 (k * years).  Using the simplified formula above, the Macaulay Duration for bond μ would be 1.7917624. 

As another example, let us assume bond φ is a $100 5-year bond compounded semi-annually with a 4% yield with a coupon frequency of 2 (payments/year), and a coupon of 20% per year.  In this scenario, y = .04, k = 2, c = 20, and m would equal 10 (k * years).  Using the simplified formula above, the Macaulay Duration for this bond φ would be 3.7813337.

In short, Macaulay Duration is the weighted average time until all cash flows are received, measured in years.  Another measure of duration that is often used is known as Modified Duration.  Modified Duration is the measure of the percentage change in price for a given change in yield.  For smaller movements in yield, the numeric results of Macualay and Modified Duration are similar; however, Modified Duration, instead of being a measure of time, is a measure of value, specifically, the rate of change of price sensitivity with respect to the percentage rate of change of price with respect to yield.

The formula for Modified Duration is:

where, in the case of continuously compounded yields:

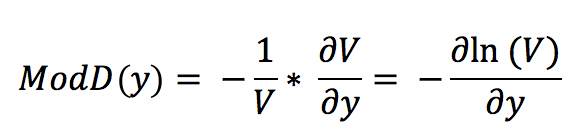
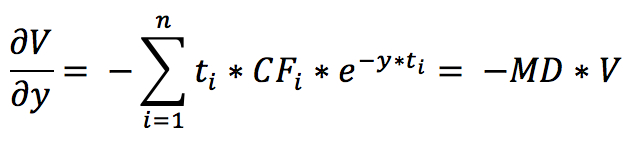
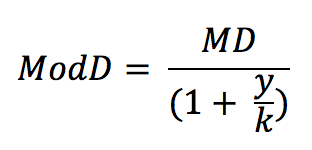
where:
            MD is the Macaulay Duration calculated for the same bond
            y is the Yield (per year, in decimal form)
            k is the integer compounding frequency

What you need to implement:

You are to design the bond class and you should incorporate for each bond the number of coupons, the coupon frequency, the yield (per year in decimal form) and the coupon paid per year in percent form (i.e., m, k, y, and c above), along with the face value of the bond (a "$100,000 bond").  Your portfolio is a composite and should be instantiated with a minimum of three individual bonds with different yields and number of years, assuming continuous compounding.  You should have two strategies for the lab, one that implements a calculation of Macaulay Duration across all the bonds in the portoflio, and another strategy that implements a calculation of Modified Duration across all the bonds in the portfolio.  Your program should instantiate the portofolio of bonds, iterate through the portfolio and print out the details of all the bonds in the portfolio, and finally print out both the Macaulay and Modified durations of the portfolio using the two strategies.  In order to print out the portfolio durations, you will need to perform a weighted sum of the durations of each individual bond in the portfolio.

In order to do this, you may assume a simple weighted average of the individual bond duration calculations and call it the Macaulay Duration for the portfolio and Modified Duration for the portfolio, respectively.  For the weighting, assume a portfolio's duration is equal to the weighted average of the durations of the bonds in the portfolio:

Portfolio Duration = w₁D₁ + w₂D₂ ...+ w_nD_n

This standard definition defines the weight as proportional to how much of the portfolio consists of a certain bond, or the percentage market value of an individual bond as a percentage of the overall market value of the portfolio.  In order to calculate the Present Value (PV) of a bond:

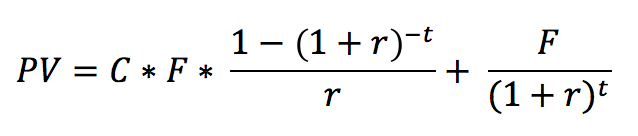
where:

C is the coupon rate of the bond
F is the face value of the bond
r is the current prevailing interest rate (you will assume r = 2.5% for all bonds in all portfolios, and may hardcode it as such)
t is the time periods occuring over the term of the bond (e.g., a two-year semi-annual bond will have four time periods, etc.)

In short, the bond's current market value is equal to the present value of the face value plus the present value of interest payments.  For example, let us assume bond κ to be a $100,000 10 year bond compounded annually (a coupon frequency of 1 payment/year), and a coupon of 8% per year.  The prevailing market interest rate we will assume is 2.5%.   In this scenario, F = 100,000, C = .08, r is .025, and t is 10 (years).  Using the formula above, the present value of bond κ would be $148,136.  As another example, assume bond γ to be a $10,000 5 year bond compounded semi-annually (a coupon frequency of 2 payment/year), and a coupon of 8% per year.  The prevailing market interest rate we will assume is 2.5%.   In this scenario, F = 10,000, C = .04 (=8% / 2 periods/year), r is .025, and t is 10 (=5 years * 2 periods/year).  The present value of bond γ would be $11,313.

You are to deliver in code a single account that contains two portfolios each of which contains three bond instruments.  The account is also to contain three individual bonds that are not attached to a given portfolio.  You should implement an Account class that uses composition to hold a root Portfolio instance representing all top level items in the account, and note that this means your Portfolio class should support arbitrary nesting. You should write an Iterator for your traversal of the Composite. It is not necessary to write a container class for your iterator, and limiting your iterator to working with something like Java built-in arrays is acceptable.

Your program should print out something like the following:

$ ./mycomposite
I am an account and I have 2 portfolios and 3 individual bonds. Account MacD is X and ModD is Y
The durations of the three individual bonds are:
bondname1 MacD is X and ModD is Y
bondname2 MacD is A and ModD is B
etc.
I also have two portfolios and the durations of the portfolios are as follows:
portfolioname1 MacD is X and ModD is Y
portfolioname2 MacD is A and ModD is B
etc.

Your exact output does not need to match the above but the above will give you a gist of what we're wanting it to do. For example, if instead of the combined approach above you want to do two separate iterations, one with Macaulay and one with Modified duration, that is fine as well.

References:

You may find the following references helpful:

An Excel spreadsheet which implements the formulas allowing you to play around with (and therefore validate) different input values.

http://cslibrary.stanford.edu/103/LinkedListBasics.pdf

http://opendatastructures.org/versions/edition-0.1g/ods-python/Contents.html

Submitting:
Submit your assignments to the subversion repository in the pre-existing folder named "labN" (where N is the homework number). Please include a README text file that contains any instructions for the TAs to assist with grading, and design notes are often the most useful thing you can provide. We do not usually need any info on how to compile your code unless your code layout is arcane.