Homework #4: Due: Tuesday August 9th, 2016 @ 11:59pm
This assignment will give you the chance to implement a game-like model from the social sciences that gives an unintuitive result.
This assignment is intended to teach you how to use
- Arrays
- Loops
- Functions
- Basic Testing
All your functions from this homework assignment should be implemented in a called hw4.c and should be placed in a hw4 directory in your repository.
Overview
Racial segregation has always been a pernicious social problem in the United States. Although much effort has been extended to desegregate our schools, churches, and neighborhoods, the US continues to remain segregated by race and economic lines. Why is segregation such a difficult problem to eradicate?
In 1971, the American economist Thomas Schelling created an agent-based model that might help explain why segregation is so difficult to combat. His model of segregation showed that even when individuals (or "agents") didn't mind being surrounded or living by agents of a different race, they would still choose to segregate themselves from other agents over time! Although the model is quite simple, it gives a fascinating look at how individuals might self-segregate, even when they have no explicit desire to do so.
In this assignment, you will create a simulation of Schelling's model. The user should be able to set a number of parameters of the model and watch it go.
How the Model Works
Schelling's model will now be explained with some minor changes. Suppose there are two types of agents: X and O.
The two types of agents might represent different races, ethnicity, economic status, etc.
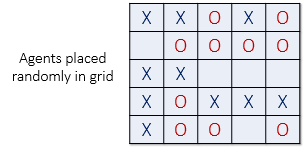
Two populations of the two agent types are initially placed into random locations
of a neighborhood represented
by a grid. After placing all the agents in the grid, each cell is either occupied
by an agent or is empty as shown below.
Now we must determine if each agent is satisfied with its current location. A satisfied agent is one that is surrounded by at least t percent of agents that are like itself. This threshold t is one that will apply to all agents in the model, even though in reality everyone might have a different threshold they are satisfied with. Note that the higher the threshold, the higher the likelihood the agents will not be satisfied with their current location.
For example, if t = 30%, agent X is satisfied if at least 30% of its neighbors are also X. If fewer than 30% are X, then the agent is not satisfied, and it will want to change its location in the grid. For the remainder of this explanation, let's assume a threshold t of 30%. This means every agent is fine with being in the minority as long as there are at least 30% of similar agents in adjacent cells.
The picture below (left) shows a satisfied agent because 50% of X's neighbors are also X (50% > t). The next X (right) is not satisfied because only 25% of its neighbors are X (25% < t). Notice that in this example empty cells are not counted when calculating similarity.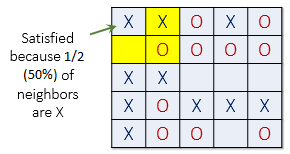
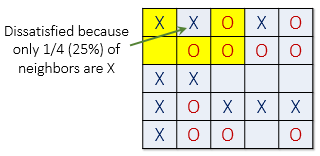
When an agent is not satisfied, it can be moved to any vacant location in the grid. Any algorithm can be used to choose this new location. For example, a randomly selected cell may be chosen, or the agent could move to the nearest available location.
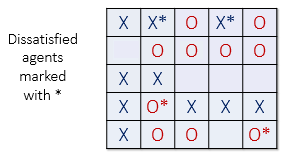
In the image below (left), all dissatisfied agents have an asterisk next to them.
The image on the right shows the new configuration after all the dissatisfied
agents have been moved to unoccupied cells at random. Note that the new configuration may
cause some agents which were previously satisfied to become dissatisfied!
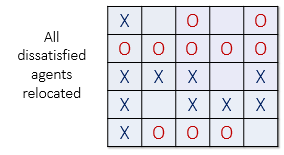
All dissatisfied agents must be moved in the same round. After the round is complete, a new round begins, and dissatisfied agents are once again moved to new locations in the grid. These rounds continue until all agents in the neighborhood are satisfied with their location.
The Assignment
In your assignment, you should do the following:
- The grid should be 30x30. You can represent the grid as a 2D character array with the agents being 'X' and 'O'.
- Prompt the user for the threshold t as stated above.
- Randomly fill the grid with the agents and empty spots. Early on you may want to make a pre-filled grid for testing purposes.
- Run the simulation with threshold as stated above.
- Print out the initial and final grid (i.e., all agents in the neighborhood are satisfied with their location).
- Ask the user if he or she wants to run the simulation again.
- Make your program as modular as possible (i.e., breaking down the program into functions and using them when needed).
Style
At the top of your C file, write a comment with your name, etc., in the following form:
/* Jane Doe, jdoe */
/* CS152, Summer 2016 */
/* Homework 4 */
Comments, where they occur, should be helpful and precise. Omit superfluous comments:
int a = b + c; /* I'm adding b and c and naming it a! */
Your code should be no more than 80 columns wide.
Do not write more than one statement on a line.
Do not submit code that does not compile. If a function is broken, and makes compilation impossible, comment out that function and submit the rest. Non-compiling code will receive little to no credit.
Submitting Your Work
Save and commit your code in YOUR-REPOSITORY/hw4/hw4.c. Recall that you will need to add your work before you commit it. (Also, notice that in the -m message you include at commit time, -m is simply a command-line option.)
Commit your work early and often. We do not grade intermediate commits, only the work as it stands at the deadline. If you have any issues with subversion, not only your instructors but your classmates can help you. Most of the students in this class have at least one full quarter of experience running subversion.
If, for any reason, perhaps due to a late add, you do not have a CS repository, save your work somewhere you can easily get it and send mail to the lecturer. We'll get you set up with a repository in time to make the deadline.
Acknowledgements
I'd like to thank Frank McCown for designing this wonderfully interesting assignment.