Combinatorics and Probability
First Midterm - April 13, 2005
Instructor: László Babai
Important. Do NOT use books, handouts, notes, scrap paper.
Show all your work.
- (15 points) Prove the Kovári-Sós-Turán Theorem:
if a graph on
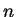 vertices does not contain a 4-cycle then
vertices does not contain a 4-cycle then
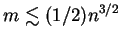 where
where 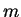 is the number of edges.
Define the notation ``
is the number of edges.
Define the notation ``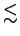 '' (``less than or asymptotically
equal to'').
'' (``less than or asymptotically
equal to'').
- (15 points) Let
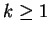 . Prove Fisher's inequality:
if
. Prove Fisher's inequality:
if
![$A_1,\dots,A_m\subseteq [n]$](img6.png) are distinct sets and
are distinct sets and
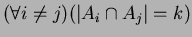 then
then 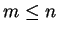 .
Define the concepts used.
.
Define the concepts used.
- (14 points) Prove Erdos's Ramsey bound:
Explain this result in mathematical English (use proper
quantifiers).
- (14 points) Esther Klein pointed out that
among 5 points in the plane, no three of which is are
on a line, there are always four which form a convex
quadrilateral. Use this fact and Ramsey's Theorem to
prove that
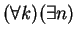 such that no matter how we
place
such that no matter how we
place 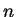 points in the plane such that no three are on a line,
points in the plane such that no three are on a line,
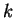 of them will form a convex
of them will form a convex 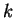 -gon. Clearly state the
case of Ramsey's Theorem you are using; use the Erdos-Rado
arrow notation.
-gon. Clearly state the
case of Ramsey's Theorem you are using; use the Erdos-Rado
arrow notation.
- (14 points) A tile is a unit square, divided into
four parts (``quadrants'') by its diagonals; each of the four
parts is colored. The sides of a tile are designated
as North, East, South and West.
We have a set of 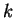 tiles and an infinite supply of identical
copies of each of the
tiles and an infinite supply of identical
copies of each of the 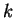 tiles. We want to tile the entire plane
(cover the plane with nonoverlapping tiles) obeying the following
rules: each tile must fill a square in the unit square grid;
the North side of each tile must point up, the East side
to the right, the South side down, and the West side to the left;
and adjacent tiles must have the same color in their adjacent
quadrants.
tiles. We want to tile the entire plane
(cover the plane with nonoverlapping tiles) obeying the following
rules: each tile must fill a square in the unit square grid;
the North side of each tile must point up, the East side
to the right, the South side down, and the West side to the left;
and adjacent tiles must have the same color in their adjacent
quadrants.
Prove: if 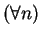 the
the 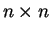 square can be tiled
in this manner then the entire plane can.
square can be tiled
in this manner then the entire plane can.
- (28 points) Prove: every triangle-free graph with
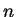 vertices
has chromatic number
vertices
has chromatic number 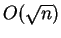 .
.
![]() tiles and an infinite supply of identical
copies of each of the
tiles and an infinite supply of identical
copies of each of the ![]() tiles. We want to tile the entire plane
(cover the plane with nonoverlapping tiles) obeying the following
rules: each tile must fill a square in the unit square grid;
the North side of each tile must point up, the East side
to the right, the South side down, and the West side to the left;
and adjacent tiles must have the same color in their adjacent
quadrants.
tiles. We want to tile the entire plane
(cover the plane with nonoverlapping tiles) obeying the following
rules: each tile must fill a square in the unit square grid;
the North side of each tile must point up, the East side
to the right, the South side down, and the West side to the left;
and adjacent tiles must have the same color in their adjacent
quadrants.
![]() the
the ![]() square can be tiled
in this manner then the entire plane can.
square can be tiled
in this manner then the entire plane can.