Boolean arithemetic is also called ``Boolean algebra,'' ``propositional logic,'' ``mod 2 arithmetic.'' The Boolean domain has only two values, which we call 0 and 1. In other books and articles, they are often called T and F. Electronically, they correspond to two distinguishable electrical values, usually voltages. When a wire or other electrical component carries a 1 voltage, our textbook says that the wire is ``asserted.''
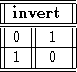
Boolean operations may be defined by tables of all their values. There are only 4 possible unary operations: constant 0, constant 1, identity and inverse. Constants and identity are trivial, and inverse has the table
We write the inverse of a as 
. In other places, it may be
written as 
, 
, or -a. Inverse is also
called, ``negation,'' or ``not.''
There are 16 possible binary operations. The two most important to us are and and or, with the following tables
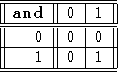
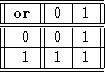
We write a and b as 
; other places it may be ab,
, 
. Similarly, we write a or b as a+b; other
places it may be a|b, 
.
Every Boolean operation, no matter how many arguments it takes, may be
defined by an expression using inverse and either one of the
binary operations and, or. It is particularly convenient
to use all three operations in expressions, and unless we say
otherwise in a special case, a ``Boolean expression'' will involve
these three operations, and occasionally the constants 0 and 1. In
fact a single binary operation is sufficient to define all Boolean
operations: the nor operation defined by 
is
sufficient, and so is the nand operation defined by
. You should convince yourself of this fact by
defining inverse, and, or in terms of nor
and in terms of nand.
Another binary operation that you are likely to see is exclusive or, given by the table
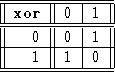
We write the exclusive or of a and b as 
. Exclusive or
is also called mod 2 sum. Both or and xor are analogues
to addition: the or treats 1 as infinity, and the xor
works modulo 2. and agrees with multiplication under both the
1-as-infinity and the modulo 2 interpretations. Notice that
Important properties of the Boolean operations include
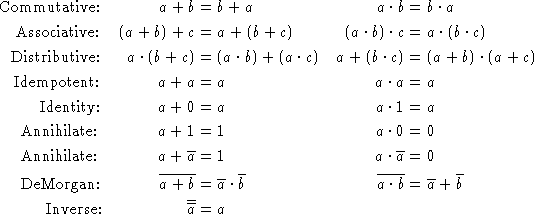
These properties resemble the algebraic properties of real number
addition and multiplication, but they are more symmetric. In
particular, the distributive property works both ways in Boolean
arithmetic. Because of the Associative law, we can skip parentheses in
long sequences of + or 
. To save further parentheses, we give
precedence over +.
The Boolean identities above can be used to simplify Boolean expressions. In particular, every Boolean expression can be simplified into a 3-level form where the bottom level has variables and their inverses, the middle level has ands, the top level has ors--alternatively we can have a middle level of ors and a top level of ands. These forms are called ``sum of products'' and ``product of sums,'' or ``conjunctive normal form'' and ``disjunctive normal form.'' Convince yourself that the Commutative, Associative, Distributive, DeMorgan, and Inverse identities are sufficient to produce normal forms. The Idempotent, Identity, and Annihilate identities can often be used to reduce the size of the normal form.
For a quick silly example,
simplifies to sum of products as follows:
Skipping unneccesary parentheses, this is
. Notice that we have sum of
products form already in line 5, then we simplify one of the
terms. You should derive the product of sums form,
, for yourself.
The normal forms for Boolean expressions are important to digital circuit design, because they lead to a technique called Programmable Logic Array for implementing an arbitrary Boolean function in a disciplined uniform way. The speed of a circuit depends mostly on the depth of the Boolean expression that it implements, so PLAs are pretty fast. But, the size of an expression may increase exponentially when it is ``simplified'' to sum of products or product of sums, so the PLA technique is used sparingly.
Mathematically, there is a perfect symmetry between sum of products and product of sums, but intuitively the sum of products is often easier to understand, because it corresponds directly to a table of the operation. PLAs in current VLSI technology use sum of products.