
The base 3 digits are represented as follows
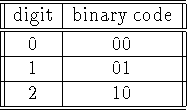
So, if ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() ,
then we are adding the trinary digit 2 to the trinary digit 1, with
no carry coming in. We never have
,
then we are adding the trinary digit 2 to the trinary digit 1, with
no carry coming in. We never have ![]() , nor
, nor ![]() ,
since those values don't correspond to a trinary digit.
,
since those values don't correspond to a trinary digit.
Write a boolean formula in sum of products form, expressing the
carry out ( ![]() ) in terms of the five input bits. You
should get a sum of six products, and each product involves two or
three input bits.
) in terms of the five input bits. You
should get a sum of six products, and each product involves two or
three input bits.

- For what values of s do the new register-memory instructions improve performance?
- Suppose that we can also add ALU operations that
combine two values from registers, but store the result in
memory (e.g., add R1 and R2, storing at address 1000 in
memory), at the cost of slowing down clock cycles by the same
factor of s. The new save-result-to-memory ALU operations
allow many store instructions to be eliminated, saving one clock
cycle for each. Which kinds of stores can be eliminated, and
which cannot? Let n be the fraction of store instructions that
can be eliminated (
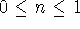 ). What relationship between
s and n causes the new design to beat the original
load/store design? If n=1, for what values of s does the new
design win? In a program that does mainly number crunching, do
you think n is likely to be nearer to 0 or to 1?
). What relationship between
s and n causes the new design to beat the original
load/store design? If n=1, for what values of s does the new
design win? In a program that does mainly number crunching, do
you think n is likely to be nearer to 0 or to 1?
- Write a program fragment consisting of a sequence of assignments in a high-level language that performs 5 integer operations. (That is, give a slightly larger example similar to the one in the statement of problem 2.3). You may use any number of variables, and you may write 5 assignments with 1 operation each, 1 assignment with 5 operations, or anything in between. Make the memory-memory instruction set beat the load/store instruction set by the largest factor that you can manage, counting total code and data. Report the total number of code bytes and date bytes transmitted for each instruction set. You do not have to write out the assembly code.
- Write another program fragment with the same restrictions as in part a, but this time make the load/store instruction set win by the largest factor that you can manage. Report the total number of code bytes and data bytes transmitted for each instruction set.
- Clearly, the relative efficiency of memory-memory vs.\
load/store depends on the program. Do loops in programs tend to
tip the efficiency balance toward memory-memory, or toward
load/store? Explain briefly (3 sentences can be enough).
- All data hazards stall until the write is finished (no forwarding of any sort).
- For branches and jumps, predict they are not taken. Cancel
the 3 instructions in the pipeline behind a branch that is
taken.
I tried to produce bad pipeline behavior. The following loop decrements R1 from 1000 to 0.
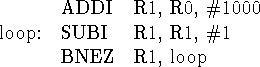
There are plenty of instructions after the loop, but we don't care what they are.
- Compute and compare the running time for this loop in the pipelined and unpipelined machines. The pipeline loses the race by a very small margin.
- Point out where data and control values already computed
in the simple DLX pipeline could be forwarded to speed up the
pipeline on this program, and compute the improved running time.