Assignment 4

Due Thursday, May 6^th in class.

Note: You'll probably want to increase the memory allocated to Matlab to 32MB (or even 64MB).

1. a) What is the result of the following convolution?

   

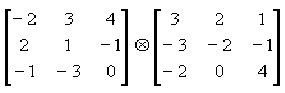
   b) Describe, in words, the result of convolving the following matrix with an image:

   0	1	0
   1	-4	1
   0	1	0

2. Use the edge function in Matlab to do edge detection on the following image:

   The image at right shows the trees we looked at in class

   a) Use the Canny edge detector with sigma = 1, 2 and 3 and compare the edges detected in each case. Why do the edge images vary?

   b) In addition to looking for extrema in the first derivative, one can also look for zero-crossings in the second derivative. One can do this and smooth in the image in two steps, because:

   

   where 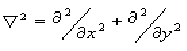is the Laplacian, G is the Gaussian and I is the image. This is the basis for the Marr-Hildreth edge detector. Use the Marr-Hildreth operator with sigmas of 1, 2 and 3 (as above) to perform edge detection. What's the difference between the edges detected using Canny, and those detected using Marr-Hildreth?

   c) Both the Canny and Marr-Hildreth operators use the Gaussian for smoothing, and hence are isotropic. Is this and advantage or a disadvantage?

3. You can use the correlation function (which you might be familiar with from statistics) to determine how closely related two sets of figures are. You can extend this to images by determining the correlation between two images, or an image and a portion of a second image. For this exercise, you should use Matlab's 2-D correlation function to determine where one of the smaller images (a moon) resides in a larger image. (Normally you wouldn't know that one image was contained in another at all -- you would need to threshold the correlation to give a yes/no answer.)
   1. Write a function (in Matlab) that will determine if an image is contained in a larger image. If the answer is yes, then it should output the location of the matching upper-left corner of the image and the matching portion.
   2. For each of the smaller images below, determine the maximum correlation within the larger image (Moon and Half Dome) and the location (within the larger image) of the maximum correlation.
   3. Is correlation a good way to find one image within another? What are the advantages/disadvantages?

      Image name		Image
      Moon and Half Dome, by Ansel Adams (From http://www.adamsgallery.com/)
      Small moon (90o)	Check whether any of these images appears in the larger image above.
      Small moon
      Larger moon

4. Use the Hough transform to find the longest line in the following image: